Gordon Stallings' Home Page
Gordon Stallings' Home PageSome current interests:
- The Battery Monitor Project
- 3-D Model of a Math Function
- An exploration of Integer Triangles
- Explorations of numbers consisting of all 1s
- My experiments with diamagnetic levitation
- CD Balls
- 24-Hedroid
Other interesting links:
Feel free to contact me.
24-Hedroid
24-HedroidHere is a model that I built that represents the "three dimensional shadow" of a symmetrical four-dimensional figure. The model is unusual because I chose to use clear plastic planes rather than just depicting the edges with a wire frame.
One way to describe this object is to say that it partitions the entire 3-dimensional space into 24 parts. Each part is a volume enclosed by eight intersecting planes. So each volume is bounded by an octahedron. Although the sizes of the volumes are not all the same and although the faces are not all the same shape and although the edges are not all the same length, these differences are distortions caused by the projection of the 4-D figure into our 3-D world. In four dimensions, all 24 octahedrons would be regular and identical. All the volumes, faces, and edges of the octahedrons would be alike if we could experience the object in four dimensions. In both the 4-D object and in my model, each volume shares its eight faces with eight adjacent octahedrons. So two octahedra share a face, three octahedra share an edge, and six octahedra share a vertex.
To count the octahedra, begin with the one in the middle. Eight octahedra touch its faces. Six additional octahedra touch its vertices. Eight more fit around those six. That totals 23. The 24th octahedron is "inside out", and consists of all the space outside of the model. Some people like to think of this model as being a "3-dimensional shadow" of the 4-D figure.
The photos do not clearly show the interior planes of the model. It is only by holding the model and turning it that a person can see all the interior planes.
This was a first attempt and I would like to build another that is more precise and beautiful. It was fun to work out the angles. The tesseract could also be modeled using this technique.
24-Hedroid




CD Geodesic Balls
CD Geodesic BallsI have found a use for those unwanted compact discs that accumulate in the house. I got to thinking that the rim of a CD could represent a great circle on a sphere. Hmmmm.... How many ways can you lay great circles on a sphere in a symmetrical manner? How best to construct these figures? What do you call them?
I have done a few. It is fun to match up the printing such that it appears that the CDs interpenetrate. I have chosen to name them according to the straight-edged figure that would result by connecting the points of intersection of the CDs with straight lines instead of curves. Only figures that have an even number of edges meeting at each vertex are candidates for these balls.
Octahedron


Three CDs intersecting at right angles. This forms "corner reflectors" with the mirror-like CDs giving the illusion of transparency to the disks.
Cuboctahedron


Four CDs corresponding to the four 3-fold axes of a cube. This figure changes appearance greatly when viewed at different orientations.
Icosidodecahedron.


Six CDs representing the great circles corresponding to the six five-fold axes of the dodecahedron. The figure has twenty equilateral spherical triangles and twelve spherical pentagons.
Stellated Cube.


24 isosceles spherical triangles. The six CDs mark the great circles corresponding to the six two-fold axes of the cube.
Stellated Cuboctahedron.

8 equilateral spherical triangles and 24 isosceles spherical triangles. The seven CDs mark the great circles corresponding to the 3 four-fold axes of the cube plus the four 3-fold axes.
Other Models
By relaxing my requirement that the CDs lie on great circles, other figures are possible. The following ones are probably about as far as I intend to go with these models for a while.
Rhombicuboctahedron.


Six CDs here.
Rhombicosidodecahedron.


12 CDs. That's enough for me!
Please contact me with questions or comments.
Exploring Integer Triangles
Exploring Integer TrianglesWhen you learn trigonometry, you learn a lot about the properties of triangles. But such understanding can lead to even more questions. This article will explore some interesting properties of triangles whose sides are integers.
Is there anything special about triangles with three integer sides, other than the fact that their sides are integers? Did you know that the common right triangles that have 45-degree angles or 30- and 60-degree angles cannot have three integer sides? Are only certain angles possible in triangles that have three integer sides? If so, can we predict whether or not an angle can be part of an integer triangle? How many different (non-similar) triangles can be formed which have integer sides and which all contain the same angle?
I will use an informal theorem/proof/discussion style to present some surprising insights into the nature of integer triangles. This will lead to Theorem 10, a clever formula for computing the lengths of sides of integer triangles having certain angles. We'll work on the most general kind of triangle, which has three unequal sides and three unequal angles. Such a triangle is called scalene.
Factors of all-ones numbers
Factors of all-ones numbersDefinition: f(n) = 10(n-1) + 10(n-2) + ... + 101 + 100
Or: f(n) = ((10n) -1)/9
f(2) = 11
f(3) = 3 * 37
f(4) = 11 * 101 = f(2) * 101
f(5) = 41 * 271
f(6) = 111 * 1001 = 11 * 10101 = f(3) * f(2) * 7 * 13
f(7) = 239 * 4649
f(8) = f(4) * 73 * 137
f(9) = f(3) * 3 * 333,667
f(10) = f(5) * f(2) * 9091
f(11) = 21649 * 513,239
f(12) = f(4) * f(3) * 7 * 13 * 9901
f(13) = 53 * 79 * 265,371,653
f(14) = f(7) * f(2) * 909,091
f(15) = f(5) * f(3) * 31 * 2,906,161
f(16) = f(8) * 17 * 5,882,353
f(17) = 2,071,723 * 5,363,222,357
f(18) = f(9) * f(2) * 7 * 13 * 19 * 52,579
f(19) = 1111111111111111111
f(20) = f(10) * 101 * 3541 * 27961
f(21) = f(7) * f(3) * 43 * 1933 * 10,838,689
f(22) = f(11) * f(2) * 11 * 23 * 4093 * 8779
f(23) = 11111111111111111111111
f(24) = f(12) * 73 * 137 * 99,990,001
f(25) = f(5) * 21401 * 25601 * 182,521,213,001
f(26) = f(13) * f(2) * 859 * 1,058,313,049
f(27) = f(9) * 3 * 757 * 440,334,654,777,631
F(2), F(19), and f(23) are prime.
Next potential prime = f(59)
Graph of X to the X
Graph of X to the X
This shape represents the mathematical function y = x raised to the x power, where x is a real number but y is complex.
The model was printed on the Dimension 3-dimensional printer.
For further information about this shape, continue reading below.

Discussion
This discussion will involve taking exponents. If you are rusty on the rules for taking exponents, see the Exponent Rules section below.
| x | y |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 27 |
| 4 | 256 |
| 5 | 3125 |
This looks like a very tame function. However, zero raised to the zero power is undefined. So xx for x=0 will remain uncalculated. See the conclusions below.
Recalling that a negative exponent represents reciprocation, we can extend the table to negative values of x.
| x | y |
|---|---|
| -1 | -1 |
| -2 | 1/4 |
| -3 | -1/27 |
| -4 | 1/256 |
| -5 | -1/3125 |
Notice that the function appears to oscillate for negative values of x. If this is the case, one might expect that there would be a value of x between -1 and -2 where y is zero.
Let’s do the math for x = -3/2.
(-3/2)(-3/2) =
(-2/3)(3/2) =
((-2/3)3)1/2 =
((-23)/(33))1/2 =
(-8/27)1/2 =
(-0.2963)1/2
Recalling that an exponent of 1/2 indicates a square root, then there are two solutions. Also, square root of a negative number causes a rotation of ninety degrees in the complex plane, indicated by the letter ‘i’.
(-8/27)1/2 =
(-0.2963)1/2 =
0.544331i, -0.544331i
So there’s the answer: The function y = xx becomes complex for certain values. Here are a couple of examples for positive x values.
(3/2)(3/2) =
((33)/(23))1/2 =
(27/8)1/2 =
3.3751/2 =
1.837, -1.837
(3/4)(3/4) =
((33)/43))1/4 =
(27/64)1/4 =
.4218751/4 =
0.8059, 0.8059i, -0.8059, -0.8059i
The previous example has four roots. This can be shown to be a general rule that the number of complex roots equals value of the denominator of the exponent.
An alternative form is to use the polar form, y = R*exp(i*theta), where R is the magnitude, “exp” is the exponential function, and theta is the angle in the complex plane. Because x is real, x = X*exp(i*pi*(0+2n)) when positive, x = X*exp(i*pi*(1+2n)) when negative, where X = magnitude of x, n= 0,1,...
Then R = X^x and theta = pi*X*(0+2n) or pi*(-X)*(1+2n).
Using that form, the four roots of the previous example become:
| R | n | theta |
|---|---|---|
| 0.8059 | 0 | 0 |
| 0.8059 | 1 | 3/2 pi |
| 0.8059 | 2 | 3 pi |
| 0.8059 | 3 | 9/2 pi |
As another example, consider x = -1/3.
y = (1/3 exp (i*pi*(1 + 2n)))(-1/3) =
3(1/3) * exp(i*pi*(1+2n)*(-1/3))=
1.44225 * exp(i*pi*(1+2n)*(-1/3))
| R | n | theta | principal theta |
|---|---|---|---|
| 1.44225 | 0 | -1/3*pi | 5/3*pi |
| 1.44225 | 1 | -1*pi | 1*pi |
| 1.44225 | 2 | -5/3*pi | 1/3*pi |
(“principal theta” lists theta values between 0 and 2*pi.)
The only remaining thing to examine is the case of an irrational value of x. Let x = -sqrt(2). Find all the values for y in polar form.
y = (1.414*exp(i*pi*(1 + 2n)))(-1.414)
y = (.70711.414)*exp(i*pi*(-1.414)*(1 + 2n))
y = .6125*exp(i*pi*(-1.414)*(1 + 2n))
| R | n | theta | principal theta |
|---|---|---|---|
| 0.6125 | 0 | -1.414*pi | 0.586*pi |
| 0.6125 | 1 | -4.242*pi | 1.758*pi |
| 0.6125 | 2 | -7.071*pi | 0.930*pi |
| 0.6125 | 3 | -9.898*pi | 0.102*pi |
| 0.6125 | 4 | -12.73*pi | 1.274*pi |
| 0.6125 | 5 | -15.55*pi | 0.446*pi |
| ... | ... | ... | ... |
This list goes on forever and the principal theta values never repeat. So an irrational x results in a ring of an infinite number of points in the complex-y-plane with radius equal to |x|x.
Because the irrational numbers outnumber the rationals, the graph of y=xx is a 3-dimensional surface with its axis of symmetry along the x axis and with its radius equal to |x|x. The surface is everywhere discontinuous except for the positive real part of y when x is positive.
Although 00 is undefined, we can write: Limit of xx as x approaches zero from positive values is equal to 1.
Exponent Rules
xa = x*x*.... (a times) = x to the ath power
Example: 25 = 2*2*2*2*2 = 32 = two to the fifth power
x(a+b) = (xa)(xb)
Example: 2(2+3) = 25 = 32 = 4*8 = (22)(23)
x(a-b) = (xa)/(xb)
Example: 2(3-2) = (23)/(22) = 8/4 = 2 = 21 = 2(3-2)
x(-b) = 1/(xb)
Example: 2(-3) = 1/(23) = 1/8
x(a*b) = (xa)b = (xb)a
Example: 2(2*3) = 26 = 64 = 43 = (22)3 = 82 = (23)2
if y = xa then x = y(1/a)
Example: 8 = 23 so 2 = 8(1/3)
x(1/b) = bth root of x
Example: 81(1/4) = (3*3*3*3)(1/4) = 3 = 4th root of 81
x(a/b) = (xa)(1/b)
Example: 8(2/3) = (82)(1/3) = 64(1/3) = (4*4*4)(1/3) = 4
Check: 4(3/2) = (4*4*4)1/2 = 64(1/2) = (8*8)1/2 = 8
Decimal example:
16(1.25) = 16(1 + .25) = (161)(16(1/4)) = 16*2 = 32
Alternate: 16(1.25) = 16(5/4) = (24)(5/4) = 2(4*5/4) = 25 = 32
Check: 32(.8) = 32(4/5) = (324)1/5 = (32*32*32*32)1/5 = (16*2*16*2*16*2*16*2)1/5 = (16*16*16*16*16)1/5 = 16
Levitation Project
Levitation ProjectHere are some notes on my approach to levitating magnets. I am using the method of suspending a small permanent magnet between two diamagnetic plates. This method of diamagnetic levitation does not involve electrical power of any sort. Nor does it use low temperatures or rotating magnetic fields.
My focus is to experiment with some of the variables involved in obtaining a stable levitation. My first experiments use bismuth as the diamagnetic material. I will provide details below but for those of you who are already familiar with this effect, I will begin with a summary of some useful things I have found out so far:
There are many other websites that contain information about this phenomenon and also have suggestions on how to do this at home.
See the following sites for a basic explanation of how to levitate a magnet.
- http://scitoys.com/scitoys/scitoys/magnets/suspension.html
- http://www.fieldlines.com/other/diamag1.html
- http://www.magnetlevitation.com
Beginning with the knowledge obtained from the above-mentioned sites, I designed my own rig. This design allows me to easily change the shape and strength of the suspending magnetic field. It also provides a way to make fine adjustments to the spacing of the elements of the rig.
The first photo shows the bare stand which is three brass rods mounted in an aluminum plate.
I had never seen bismuth before. It is a metallic element which is not quite as dense as lead and is white with a pinkish tinge. Bismuth is crystalline and rather brittle and it expands as it solidifies. It amalgamates with lead so I embedded tinned copper wires into the casting so that I could support the upper repeller. It is important to keep the copper away from the center of the casting or else make sure it is deeply embedded because copper is not diamagnetic. The casting was done in the bottom of a pop can as described in the above references. This photo shows the upper repeller on the stand.
French-fry your bismuth
There are some tricks that will make it easier to cast the bismuth repellers. The bismuth as obtained is in the form of black spheres. These spheres need to be melted together in order to form a flat surface for repelling the magnet. When the bismuth is melted, the black oxide (dross) floats to the top of the liquid metal where it can be scraped off. But more oxide begins to form immediately due to air contacting the liquid metal surface. If you put some Crisco or cooking oil onto the bismuth and then melt it, the oil floats to the top of the metal and seals out the oxygen. Also, the dross floats in the oil and is easily removed. Thus you can obtain very clean and shiny bismuth for casting.
Another trick is to melt the bismuth in place. To do this, cut some openings in the side of the pop can, put the bismuth shot and oil into the well of the can, and use a small propane torch to heat it from underneath. Once it is molten, try to cool it differentially from one side. That is, keep one side warmer while the other side solidifies. This has the advantage of providing one spot where the upwelling will occur. Bismuth is an unusual material because it expands when it solidifies. This means that the mirror-smooth surface of a puddle of liquid bismuth will be overlaid with a messy upwelling as it cools. If you can keep the upwelling on one edge, then the rest of the piece can remain flat and highly reflective. There will be crystal patterns in the surface but they will not detract from its reflectivity. The finish will be flatter and more perfect than that which can be obtained by polishing. It is nice to have the mirror finish because the reflective surface helps to display the floating magnet. Warning: Such a surface is very easily scratched by even a very soft cloth. So to retain a flawless finish, DON'T TOUCH. Of course, you can always remelt the bismuth and try again.
This photo shows a magnet levitating in the rig. The rig makes it easy to experiment with variations of the positions of the components. The lower repeller is sitting on a white plastic bottle cap. This makes it easier to remove and adjust. The mirror finish of the lower bismuth repeller makes the air gap between the magnet and the bismuth very obvious. Notice that I am using just one cube magnet on the top deck to provide the magnetic field that will counteract the weight of the levitating magnet. A cheaper magnet can be used but the deck will need to be lowered somewhat.
Potential Energy Graphs
Here is an easy way to understand what is going on. Let's look at the potential energy of the tiny cube magnet. Without the bismuth repellers, a graph of height (horizonal) versus potential energy (vertical) looks like this.
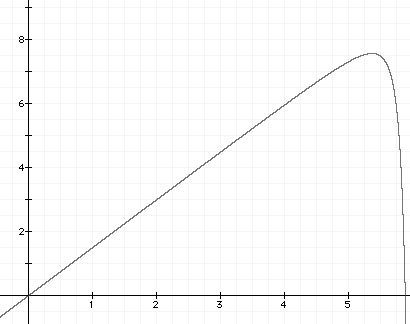
Potential energy rises linearly as the magnet is raised. But when it gets near the supporting magnet, the pull causes a rapid drop in potential energy. Notice that the top of the "knee" on the graph is smoothly rounded so that there is no position which is stable. The top of the curve corresponds to the familiar "neutral" feeling when forces just balance.
The diamagnetism of bismuth delivers a small repulsion when a magnet comes near. A single repeller can create a small stable region if it is placed near the point of maximum potential energy. The following graph shows the use of a lower repeller.
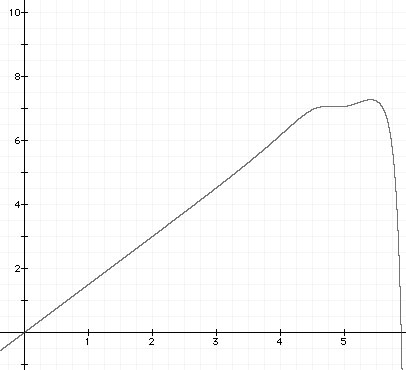
According to the graph, the magnet will be stable in a region where almost all of its weight is cancelled by the suspending magnetic field so that the repeller can deliver the remaining push for levitation. This region exists but is very touchy. By using both lower and upper repellers, the following graph can be obtained.
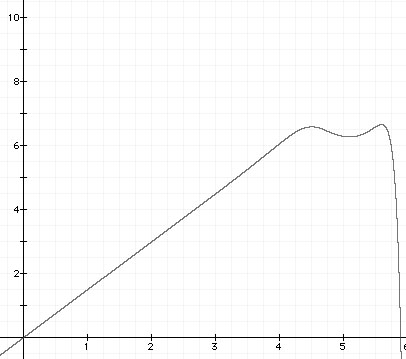
If the magnet rises, it is pushed down by the upper repeller. If the magnet moves down, it is pushed up by the lower repeller.
The magnet can also float freely below the upper repeller without the lower repeller. But if the magnet ventures too far below the repeller, it falls because it reaches a weaker part of the suspending magnetic field which cannot support the entire weight of the magnet.
Spread out your field
I found that the gap between the upper and lower bismuth repellers can be increased if the supporting magnetic field is spread out. One way to do this is to use many magnets with their poles all aligned in the same direction. I made this magnet stack by gluing the first level of magnets onto the plywood board. (The magnets must be glued because otherwise they will flip due to repulsive forces.) Warning: cheap ceramic magnets such as those shown may not deliver uniform fields. Each magnet can be tested by using some "magnetic viewing film", available from http://www.wondermagnet.com
Using this magnet stack, I can obtain a gap about 1mm above and 1mm below a levitating magnet. So the effect is most dramatic if I use small magnets. I'm floating 2.3mm NdFeB cubes (gold-plated).
This arrangement suspends a magnet in a fairly sizeable potential well in 3-space. The stable region is a cylindrical volume 4mm high and about 40mm in diameter. Vertical period of oscillation is about 0.7 sec, horizontal period is about 1 second. (3-D Lissajous figures!) So it can be used as a very sensitive detector of magnetic properties of materials. For instance, by bringing a pencil point near the levitating magnet, I have found that pencil "lead" is paramagnetic. That is, it slightly attracts both poles of a magnet. This is surprising because pure graphite is supposed to be diamagnetic and thus repel like the bismuth does. Perhaps it is the clay binder in the pencil lead that causes the effect.
Using this broad field, I can put two cubes into the levitator simultaneously. Since the levitated magnets have their poles aligned, they repel each other. The repulsion is balanced by the gradients in the field so that two magnets will lie equidistant from the supporting field's central axis. (14mm separation) I can even put three magnets into the device if I'm careful. But they lie at the vertices of an equilateral triangle 23mm apart -- just inside the edges of the bismuth repellers. So four magnets are out of the question with the current repellers.
Future Work
How thick does the repeller need to be?. Can I increase the gap by using thicker bismuth? Can the bismuth be shaped to act like a "lens" to improve the properties of the stable zone? Can I modify the supporting field to further improve the stable zone? What about putting a steel plate or magnets beneath the rig to make the magnetic field more uniform?
Another question that comes up is, "Can a piece of soft iron be used in place of the levitating magnet?" Soft iron responds to a magnetic field by becoming a temporary magnet itself. But its magnetic character depends upon the external field. So a piece of soft iron in the rig would certainly not work against the lower repeller since its strength would drop as its position drops so that the repulsion would lessen as well. But there might be some hope using just the upper repeller. I have not yet done this experiment.
I will post my answers to these and other questions as I continue experimentation.
Although the diamagnetic effect is small, it provides some interesting effects. I can even feel the reduced friction when putting a strong magnet against the surface of the bismuth. Practical uses may be found for this effect.
You can contact me with questions or comments.
Monitor All Batteries at Once
Monitor All Batteries at OnceIntroduction
My Solectria Force electric vehicle has thirteen 12-Volt batteries connected in series. Although measuring the voltage of the entire string can tell you if there is a problem, it doesn't isolate the trouble to an individual battery. The Solectria owner's manual recommends load testing the batteries once a year. This test requires a block of time and considerable work. The battery compartments must be opened and each battery's voltage measured.
It would be much more convenient, and safer too, if this test could be done without the effort and hazards involved in accessing the battery chambers. Even better, if the metering were in the passenger compartment, then the driver could evaluate the dynamic performance of each battery under actual driving conditions. I have designed and built such a device, which I will describe below.
One simple way to monitor the voltage of multiple batteries would be to use a voltmeter and a multiple position switch. Figure 1 is a schematic of such an arrangement with four batteries.
![]()
This arrangement requires the batteries to be separate and to share a common connection. However, most battery systems are series connected.
The diagram in Figure 2 uses one voltmeter and a two-pole multi-position rotary switch to select the battery to monitor. While accomplishing the goal of bringing the metering of batteries out of the battery compartment, this design has some safety problems.
![]()
A direct connection to any point in the battery pack is dangerous because of the shock hazard and also because a short-circuit could result in injury or fire. The risks can be reduced by revising the design as shown in Figure 3.
![]()
By placing current limiting resistors right on the battery terminals, only micro amperes are allowed to flow on the wires of the instrument, even in the case of a short circuit. Note that the meter itself is not a voltmeter but is a micro ammeter with a scale marked in Volts.
Citicar Design
If the switch is eliminated by providing separate meters for each battery, then the batteries can be compared under identical load conditions. In 1989, I installed just such a meter system in my Sebring-Vanguard Citicar. The dashboard sported eight vertical panel meters, one for each 6-Volt battery. I included trimmer potentiometers behind the dash to provide calibration of the meters. Figure 4 is the circuit diagram for one meter.
![]()
These meters did an excellent job in the Citicar. It was easy to spot a weak battery and individual cell failures were immediately evident by the 2-Volt drop in the meter. I wanted to have similar metering in the Solectria Force.
Designing the System
The dashboard appearance of the Force would suffer if I installed thirteen meters of any sort. But there is room in the instrument cluster for one small instrument. I decided to make a display which could show all 13 batteries at once in bar graph format. So the challenge was to design something that could continuously display the voltage of each battery altogether in a compact space on the dashboard. Figure 5 shows what I had in mind.
![]()
The numbering below the bars identifies each battery. The numbers 1 to 8 identify the batteries in the rear set and the letters A through E identify the five batteries under the hood. The height of a bar indicates the terminal voltage of that battery. The display is "live" so that a change in battery voltage results in a corresponding change of bar height. In the example above, battery C has low voltage.
I evaluated several alternatives before settling on a design. My goal was to build a system that is simple, safe, cheap, reliable, accurate, and responsive. As with any design, there were some tradeoffs to be made. The resulting design met most of my goals. I will describe a few of the reasons that I made certain design choices.
The Display
It is difficult to find a display that will fulfill my idea for a bar graph display. I considered using some sort of LED bar graph unit as found on some stereo systems. Eventually, I located a liquid-crystal display of the proper size for the dashboard installation. This display, a Densitron LM4064, is point-addressable, 64 by 100 pixels. Its exterior dimensions are about two inches square and one fourth inch thick. The display operates using standard 5-Volt digital logic, so there must be a conversion from the analog battery voltage to digital values. Fortunately, a huge assortment of digital devices can operate with the display.
The Converter
There are analog-to-digital (A/D) converters available which include switching for monitoring multiple voltages. The switched input scheme is called a multiplexer (mux). So an A/D with mux could replace the voltmeter and switches in the first drawing, above, but only if the batteries are not connected in series.
The Isolator
I located an optical isolator which serves a key role in the design. Imagine a small lamp connected to each battery. The brightness of the lamp would depend upon the voltage provided by the battery. If the light from the lamp falls onto a photocell, then the photocell's electrical output would represent the battery voltage. The higher the battery voltage, the brighter the bulb, the higher the photocell output. The advantage of this scheme is that the photocells are electrically independent and do not have to be connected in series. In particular, they can be connected with a shared common point, as shown in the Figure 6.
![]()
In this diagram, the voltages E1 through E4 are suitable as inputs to an A/D converter, each one respectively representing the voltages V1 through V4 of the batteries.
The PS8602 is an optical isolator which performs the desired function. It delivers analog output for analog input. This makes it possible to get all battery readings referenced to the same electrical common point. By using these isolators, analog-to-digital conversion is much easier and safer as well.
In Figure 7, V is linearly related to the voltage across the battery but it is electrically isolated from the battery.
![]()
The variable resistor provides adjustment to make sure that all channels deliver the same V for the same battery voltage. I used two 1k resistors to limit the current into pins 2 and 3. When I adjust the variable resistor to deliver 1 Volt at point V when battery voltage is 15 Volts, I obtain the curve in Figure 8 as battery voltage varies.
![]()
Notice from the graph that output voltage decreases as battery voltage increases. This reverse behavior can be corrected by the computer.
The Computer
The task of operating multiple-channel analog-to-digital (A/D) converters and then arranging dots on the liquid-crystal display in the desired pattern is an obvious job for a computer. I used a Basic Stamp2, which has enough input/output (I/O) lines to control the display and the A/D converters. There are some very nice A/D devices which are designed to work well with small computers like the Stamp.
The Resistors
With 1k resistors at the battery terminals, the current through each resistor is about 6 milliamperes. However, a worst-case short-circuit between two sensing wires in the rear battery compartment could place 96 Volts across 2k ohms. For the resistors to tolerate this condition indefinitely, they would have to dissipate about three Watts. I did some tests with 1/4-Watt metal-film resistors and found that they tend to blow apart under overload conditions. So in the unlikely event of a short in the sensing wires, a resistor will serve as a fuse.
The resistor fits inside the collar of a ring lug, providing a very convenient way to install the resistors and connect the sense wires.
![]()
The Design
The A/D unit I chose will handle eight channels of analog. It includes a serial interface for communication with the computer. The batteries in the Force are arranged 5 in front, 8 in back. So the design naturally breaks into two "sensor boxes" near the batteries and a "dash unit" in the dashboard instrument cluster. The Basic Stamp computer is in the dash unit. A small cable interconnects the units. Twisted pair wire is used for the short length of sense wires connecting the resistor lugs to the sensor box. This reduces the influence of stray electrical fields on the analog signals.
See the Cabling Schematic for the final design plan. All schematics are shown at the end of this article.
The battery box contains the optoisolators, the A/D mux and a voltage regulator. There are also adjustable resistors for each channel to provide single point calibration. This adjustment compensates for variation between resistors on the battery lugs, differences in isolators, etc. By using a voltage regulator in each sensor box, noise coupling on the power lines is eliminated.
The dash unit consists of only the display and the Basic Stamp2 computer. The Basic Stamp includes a voltage regulator which can accept the regular 12 Volt accessory power. This regulator has enough spare capacity to support the power needs of the liquid-crystal display as well.
Implementation
I used Express PCB, a web-based printed circuit board manufacturer to have custom circuit boards made for this project. This greatly simplifies construction for a modest price. The battery box boards fit into a commercial box from Serpac. The end panels on the box mount multi-pin connectors. I put a DB-25 on one end to provide the connections to the twisted pairs that bring the analog signals from the batteries. On the other end, a DB-9 connects the box to the plenum-grade ethernet cable that carries signals between the battery box and the dash unit. This cable also delivers the 12 Volt power to the battery boxes, but that power is only provided when the dash unit is plugged in. See the schematics for details on this.
I also used a printed circuit board to mount the Basic Stamp behind the display. The display and computer assembly fit snugly into the instrument cluster behind a hand-made mounting bracket. Space is limited in the dashboard, so the only connector on the printed circuit board is the one that accepts the end of the flex cable from the display. Cables for interfacing to the sensor boxes are soldered directly to the printed circuit board and terminate in connectors behind the dash.
The bezel for the display is cut from the original plate that Solectria put into the dash. This gives a very professional look to the installation.
![]()
Calibration
An instrument is only as good as its calibration. So this step is critical.
Each channel of analog signal must be calibrated so that the final display indicates the true voltage of each battery. One way to do this is to connect the cabling and resistor/ring lugs to the sensor box. All positive leads are connected together on one bolt, and all negative leads are connected together on a separate bolt. By applying a known voltage to the two bolts, all of the isolators will be energized under identical conditions. This voltage should be "pure" DC. Any ripple in the power will result in poor calibration. To calibrate a channel, I connected a voltmeter to the output of an isolator and adjusted the output voltage by means of the 10-turn potentiometer for that channel. A dab of fingernail polish on each potentiometer prevents setting drift due to vibration.
![]()
I provided test points on each isolator's output to make this measurement easy. I chose to set all channels to deliver 1.50 Volts out when 13.5 Volts are applied at the ring lugs. This keeps the isolator in its linear region and guarantees that all healthy batteries will show the same reading on the display. However, this is a single point calibration and so it does not correct for any variation in the performance of individual isolators. Since the display is only qualitative, I did not bother to deal with this. But it could be done with additional programming.
Programming
The Basic Stamp 2 proved to be an ideal computer for this project. Its BASIC-like language is simple to learn and it can handle bits, nibbles, bytes, and words as needed. I used the BS-2 Starter Kit to connect the Stamp to the A/D converter. Once programming was developed that could communicate with the A/D, then I did the same thing for the liquid-crystal display. The BS-2 has enough program and variable storage for this project and it consumes less power than the fancier Basic Stamp models.
The final program listing for this design fills a little more than two pages of paper. It performs the following tasks when power is applied:
- Erase the display.
- Write the numbers and letters along the bottom.
- Begin Loop
- For each channel,
- Request the value from the A/D mux for that channel;
- Display the bar height corresponding to the A/D value.
- (next channel)
- For each channel,
- Repeat the Loop
The program repeats the loop as long as power remains on.
Performance
The bar height represents a voltage range from 5.5 Volts to 18.5 Volts. This covers the voltages of interest and provides good resolution. One pixel of bar height represents about 0.25 Volts. The program loop time is less than one second. This means that changes to battery voltages due to acceleration or regeneration show up on the display very quickly.
The display not only shows the condition of the batteries. It also shows the condition of the battery connections. If a battery's voltage is excessive during regeneration or charging, it may indicate a loose terminal connection.
Retrospective
On a scale of one to ten, here is my evaluation of how well I met my goals.
- Safe: I would give it a "9". The chances of a fault that would bring the battery power into the passenger compartment are very small. I mounted the sensor boxes in protected areas so that they would not be the first thing to be crushed in an accident. A short-circuit in the sensor wiring might cause a small fire at the battery lug before the resistor burnt out. But the wiring has been kept short and it is protected from any contact with sharp edges that might fray the insulation.
- Responsive: 8. The loop time for the computer is slow enough that a sudden change of load on the batteries will show up as a "ripple" on the display. But it is not so slow as to be annoying.
- Accurate: 7. Single-point calibration does not compensate for the differences in "gain" of the different optoisolators. Consequently, the bars do not "track" completely when voltage moves away from the calibration value. This only amounts to about one Volt difference when the input voltage drops to six Volts. This would be a problem if the vertical scale were marked. Several things could be done to improve the accuracy. One way would be to select matching optoisolators from a larger set. Another approach is to do a two point calibration. This requires some programming to make the computer compensate for differing slopes on different channels. For my purposes, I feel that the accuracy is sufficient. In particular, when driving with a healthy battery pack, all of the channels stay together very well over the voltage ranges that are spanned between heavy regeneration and heavy acceleration.
- Reliable: 8. The instrument is solid-state except for the display. It consumes very little power and operates well over the temperature range that I experience. The weakest link is probably the display. I was unable to obtain the display that I wanted and had to settle for the "commercial" temperature range of 0 to 50 degrees Centigrade. The wide-temperature-range unit is rated for -20 to +70 degrees Centigrade, which is more in line with the automobile environment. Conditions of condensing humidity can also damage the display. I am hoping that the display's location inside the instrument cluster will reduce the risk of a humidity short-out.
- Cheap: 6. This is a tough one. Parts cost was about $500.00. If my labor were included, it would be much more. This is to be expected for a single unit construction (no mass production). I feel that it is very much worth the cost and time involved to have such a cool and useful instrument in the dashboard. There are costly commercial units available which do a similar function but they do not mount in the dash. .
Conclusion
It is always a thrill to design and bring to life a combination of hardware and software. Even after exhaustive study of the data sheets of the components, it is almost certain that the first configuration will not work at all. But with perseverance, all the problems and mistakes can be found and corrected simply by changing the program statements or revising the wiring connections. Step-by-step, the project fell into place and even the bezel that covers the mounting of the display worked out perfectly.
The design is easily adapted to different installations. Other than the printed-circuit boards and the software, everything is off-the-shelf. The sensor boxes are quite general and can sense any battery voltage by using appropriate resistors. The sensor boxes can be interrogated by any computer that has digital I/O lines. A point-addressable display can be programmed to show the data in a variety of ways.
Schematics
![]()
![]()
![]()
![]()
Parts Lists
For parts list, computer program listing, etc., contact me.